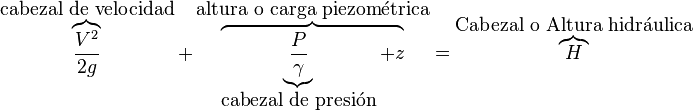Hidráulica General y Aplicada: Ecuación de Bernoulli

La ecuación de Bernoulli, también llamado "Principio de Bernoulli", supone en un principio la inexistencia de perdidas locales y globales, haciendo una igualdad directa entre energía aguas arriba y energía aguas abajo:

$\overbrace{{V^2 \over 2 g}}^{\mbox{cabezal de velocidad}}+\overbrace{\underbrace{\frac{P}{\gamma}}_{\mbox{cabezal de presión}} + z}^{\mbox{altura o carga piezométrica}} = \overbrace{H}^{\mbox{Cabezal o Altura hidráulica}}$ Es decir que la altura hidráulica aguas arriba y aguas abajo debería ser la misma. Esto se da compensando los parámetros de la manera apropiada.

Si bien el resultado de esta igualdad no es del todo errado, induce un error por no considerar las pérdidas locales y globales. Para minimizar el error se plantea la siguiente ecuación:

$\frac{{V_1}^2}{2 g}+\frac{P_1}{\gamma}+z_1 + W = h_f + \frac{{V_2}^2}{2 g}+\frac{P_2}{\gamma}+z_2$

Donde se plantea un término para las diferencias de energía por pérdidas y por ingreso o sustracción de energía al sistema.

Hidráulica General y Aplicada

martes, 24 de marzo de 2015

Ecuación de Bernoulli

No hay comentarios:

Publicar un comentario